In the spotlight last week, Aberdeen and Havre de Grace high schools were recognized for outstanding student achievement in a national program to improve results on Advanced Placement Exams in math, science and English. Here’s a look at the 2013 Advanced Placement results for all subjects in each of the ten Harford County public high schools. But first, a brief review.
About Advanced Placement (AP)
The College Board develops Advanced Placement exams and offers them nationwide each May in over 30 subjects including English, calculus, history, foreign languages, sciences and the arts. Because AP exams test high school students on a college level, passing an exam is considered an indicator of college readiness. Many colleges also offer credit for passing scores.
In preparation for AP exams, specially qualified teachers use course content approved by the College Board to teach AP courses in high school. Students can take AP courses and exams in more than one subject. However, students enrolled in an AP course are not obligated to take the corresponding exam.
2013 AP Results in HCPS: Participation Soars; Passing Rate Flat
As previously reported by HCPS, total enrollment in AP courses and AP exam participation soared in 2013, jumping by 28% and 25%, respectively, compared with 2012. The results continue a significant upward trend in AP participation in recent years.
The average passing rate on the exams dipped in 2013 to 63% from 64% in 2012.
AP Subject Offerings in HCPS
The number of AP subjects offered in a school depends in part on student interest and teacher availability. A total of 26 AP subjects were offered among the ten county high schools in the 2012-13 school year, down one subject from the previous year.
C. Milton Wright High School offered the greatest number of AP subjects (24) followed by Aberdeen (22) and Bel Air (20).
The fewest were offered at Edgewood (14) and Havre de Grace (14), Joppatowne (12), and Harford Technical High School (6).
Test Me, Test Me Not
Students who do not expect to earn a passing score are likely to opt out, but there are other reasons why students may take an AP course and not the exam. For example, not all colleges grant credit for passing scores, and some students take AP classes for the challenge alone, or to boost their high school grade point average (grades earned in AP classes have a higher point value than non-AP grades). Lastly, because the College Board charges a fee of $89 per exam, cost can be a barrier, although waivers are available for students living in poverty.
Overall in HCPS, approximately 66% of those who enrolled in AP courses took the corresponding AP exam in 2013, up from 64% in 2012.
AP students at Harford Technical and Aberdeen high schools took the exams most often, opting to take the exams 83% and 82% of the time, respectively.
AP students took the exams least often at Fallston (54%) and Patterson Mill (49%).
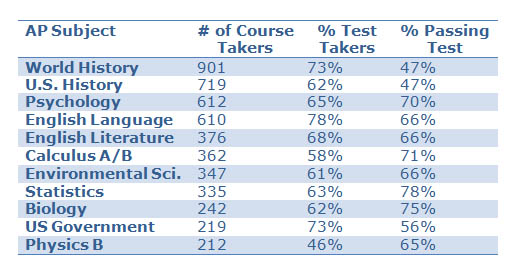
Among the most popular* AP courses system wide, the following table displays the percentage of students enrolled in each subject who opted to take the corresponding AP exam, and the passing rate among test takers.
Source: HCPS data, compiled by The Dagger.
* Ranked by enrollment. Please note that students may take more than one AP course—HCPS counts each course as a separate enrollment.
2013 AP Results by High School
New in 2013, students at Aberdeen and Havre de Grace high schools were paid $100 for each passing exam in math, science and English, through their schools’ participation in a program under the National Math and Science Initiative. The program targets schools serving military families, and also includes training and incentives for teachers, plus other supports.
Overall in 2013, the highest average passing rates in HCPS were at C. Milton Wright (77%) and Aberdeen (68%) high schools. The lowest were at Edgewood (40%) and Joppatowne (30%).
Below are the AP results by subject at each Harford County high school, plus the alternative education program at the Center for Educational Opportunity (CEO) in Aberdeen. The data was provided to The Dagger by HCPS.
Please note: To protect student privacy, whenever AP courses or exams were taken by fewer than five students, exact figures were not provided by HCPS. Instead, the data boxes on the chart below were colored yellow. Blank (white) boxes indicate where AP subjects were not offered in certain schools. Please remember that students may take more than one AP class; HCPS counts each class as a separate enrollment.



These statistics are rendered useless unless the variable, “Number of sections” is factored in.
2 schools could have the same number of test takers in a given subject, but if one has 20 per class and the other has 30 per class, there will ultimately be a difference in the passing rate.
Go figure, History and Government classes are the worst academic scores.
It’s painful to see how poorly Joppatowne H.S. is doing. Some years ago, it was actually a “Blue Ribbon School.” What has happened to it?
If you were a teacher, would you want to work at C Milton Wright or Joppa?
Risk of getting a chair thrown at my head, or work with parents who push their kids to succeed? Hmmm…
What happened to the demoted principal at Bakerfield. They moved him back to teacher. Why does he still have a job?
Maybe he’s a good teacher but a lousy administrator?
Usually it’s the other way around. Most Administrators were lousy teachers; and then they evaluate them! That shi* cray!
Maybe HCPS should use peer evaluation?
It quickly weeds out the slackers in private industry, and gives much more insight than a polished and planned-for-weeks event staged for a visiting observer.
Teachers do not know when they are going to be observed by their administrators. There is no “staging” of a lesson for an observation.
The evaluation process has also changed significantly this year with a new rubric for classroom observations, the incorporation of student growth (with evidence) in both student learning objectives (SLOs) and a teacher selected assessment as components of the evaluation, and professional development plans that must be approved and monitored by administrators. The process also demands each teacher meet with their administrators at least three times a year (instead of only once or twice in the old evaluation system) to discuss the teacher’s SLOs, self-assessment, and professional development plan.
Your continued criticism of teachers and how they are evaluated would be more valuable if you actually knew what you are talking about instead of just spouting your biased opinions.
Kharn is clueless:
Observations vary from school to school; Administrators in some schools will announce their observations, while others will try to catch teachers “off-guard.” What is worse is when Administrators in some schools will make most of their observations unnannounced, while hooking their teacher-friends up with an inside tip.
Let’s push to get video capturing devices be installed in each classroom for the purpose of employee evaluation, and liability for the employee.
If you aren’t doing nothing wrong then you have nothing to worry about.
When did that happen? Where and what is he now teaching?
What does the principal at Bakersfield have to do with this article. Lets stay on subject AP scores. Great job Aberdeen. Find the statistics interesting. Take Biology and the enrollment at AHS and compare to Bel Air. Look at the number enrolled and being successful. I thought BAHS had this bio medical program. Why are there so few kids taking AP Biology at Bel Air. I guess the kids at AHS are more into the math and sciences. Great Program too bad the school board has cut bus service and are making it so difficult of some of harford counties best and brightest being able to get to the school. Way to go school board lets destroy a great program.
Another variable that is missing in the statistics: Which schools push their students to take the exam, and which don’t.
Which is more important: the number of kids passing the exam, or the number of kids taking the exam? See: A.P. Physics at Bel Air & Aberdeen.
The former principal at Bakerfield is a teacher at Prospect Mill Elementary School. The rumor mill says that he overspent and allowed teachers to use sick days for vacations. It is strange that the former principal at John Archer did physical and mental damage to teachers and students, but was not humiliated like the former principal. Gee, I wonder why???? It is so easy to figure out in this county. The new principal at Bakerfield…..well, let’s just say she is only in it for the money. She has no concerns about student achievement or the well-being of her staff. Good luck.
Seriously, do you know her well enough to make that call. Have you looked at her past record of performance or spoke to any parent at any school she has worked before?
Another reason to only award certain employees of an employer with a raise.
Suppose if one school is at the bottom of the barrel with poor academics, why sould those employees get a raise with.employees of other schools that have better academics? Obviously poor academics means poor performance, all around.
You simply do not understand the dynamics of K12 education. The most telling predictor of the academic success of students can be directly applied to the zip-code in which they live. If you have students that come from economically affluent and stable families they do better in school. There are exceptions to this on an individual basis but it takes an extremely diligent parent(s) to overcome the economic disparity. Being an educator I can tell you that there are significant numbers of teachers in the “better” schools teaching very good students in upper level classes that would not meet with the same success if they were teaching in one of the lesser performing schools. Following your theory teachers in the more difficult schools would never get a raise and no teacher would ever want to teach there.
So dentists in WV should get paid less than those on floridated water?
Raises for HCPS employees are all or none– certain teachers at certain schools don’t get raises when other employees don’t. All teachers get raises, or none of them get raises. It doesn’t matter which school the teacher is at.
Ed Yuatamint
I would agree with you and the physics numbers at AHS and BAHS. Maybe the kids at Aberdeen feel more confident in their knowledge and what they have learned thus the higher number of kids taking the exam. Might just be the total depth of the program they have taken part in.
I would bet that if you subtracted the Math and Science Academy students from the equation you would find a different set of numbers for AP results at Aberdeen. The same would apply to the IB students at Edgewood. Remember the students in these programs have applied, been vetted for prior academic success, and hand picked by the school system. They are already extremely motivated and have extraordinary parental support, which makes all the difference.
Edgewood does not have a lot of takers because they take the IB tests instead.
Aberdeen has an enrollment of 1464, and 162 were honored on Friday. What I don’t understand is how can Aberdeen be qualified for being #1, in the nation if only 11% of their students were honored?
If you read the press release, you would know exactly what the reason is. It is very explicitly written that of all the schools receiving NMSI grants, AHS had the highest increases in AP test takers and test “passers”.
Concerned Teacher,
Oh as if I didn’t see that, but thank you for bringing that to my attention, LOL. My point is/was that it is very misleading to parents, public, and community to hear/see that Aberdeen High School is #1 in the Nation. When in reality Aberdeen High School, as a whole, isn’t #1 in anything, other than maybe BS.
What would you expect them to do? Put an academic magnet program at a successful high school? Don’t be ridiculous…
Glorified magnet school results you say? They do well because the students want to be there, take away the “route 40 want to be there’s” and what do we got?
This is a very revealing article. I especially appreciate the statistic for number tested, given the misplaced emphasis from administrators on how many of their students are enrolled in an AP course.
It would be very instructive to go deeper into the numbers for “percent passed,” which I assume HCPS means scored a “3” or better. In fact, Educational Testing Service refuses to use such a designation and merely refers to a “3” as “college qualified.” The more competitive colleges seldom grant credit for a “3, ” which is not terribly hard to achieve. Better colleges and universities usually require a minimum “4” (well qualified); many demand a “5” (very well qualified).
A truer measure of achievement within a high school would be percentages of 3’s, 4’s, and 5’s.
I agree, selective reporting makes HCPS look good while the students get to repeat the class.
Devil is in the details, so what you’re trying to say in most politically correct as possible is that a bel air-ish school is better than say, an Edgewood-ish school? Yeah, uh, we all know that.
The one thing we can’t have in a big blue state is a shitty school system, the magnet programs are a “social” blessing in disguise!
In case you missed he last couple of years in 4-year, for-profit schools, Advanced Placement exams are being rejected more and more each year. Not only is profit on the line for institutions, but studies are showing that when they were accepting AP, students were still behind than what colleges needed to go on to follow-on classes. This could also be biased most likely by the profit discussion once again.
Add the fact that the college dropout rates are increasing, http://www.oecd.org/edu/eag.htm . AP exams are great for students if the universities accept them, but they are far from a measure of how successful a student will be in college. The numbers say the opposite. I would take a student coming from a 2-year community college into a 4-year program any day. This is the model which is showing more success while providing cost savings in estimates of 30-40% in some cases.
Unfortunately it may only be a matter of time before the for-profit universities jump onto the 2 year Community College trend and adjust cost accordingly to stack the dollars.
You can keep sitting on dagger and thinking school reports, especially from Harford County Public Schools reporting, are going to show you a mirror of student performance in college, but frankly you’d be better off continuing to smell your own flatulence.
Can you provide a list of those schools rejecting AP credits? Certainly not UMD. My son entered college with 32 credits (4 on one AP test and 5’s on the others). He’s been very successful in college with a STEM major. Lest you think he’s the exception, his friends are doing likewise. Of course, they all attended the local high school whose students excel in taking a great number of AP classes AND tests. Where the students don’t get paid but are blessed with outstanding teachers.
I think another telling thing is how many AP classes had ten, or even five, students enrolled in them.
In today’s budgetary environment, some reality needs to come into the system. HCPS should only offer AP classes when there are 10 students willing to enroll and seriously reexamine the future of AP classes with low passing rates.
We also need to look at *why* some of these classes are so small. AHS is obviously going to have a high AP enrollment due to the SMA and Edgewood will have few IB students taking the AP tests (leaving the non-magnet EHS students to take the AP tests on their own, showing honest numbers for once). But there are some puzzling ones:
CMW had 59 students in AP biology, PMHS could only muster 10 and JHS could only get 8?
What is the difference? Is it the teacher? Rumors of past success? Are students at PMHS and JHS having a poor experience in the non-AP bio course that they feel the AP version is not worth the effort?
Why can CMW, FHS, NHHS and PMHS all find 12+ students for AP Chemistry, but BAHS, EHS and HDHS can’t find 10. And why can’t Joppatowne find even 5 kids to take the class? What are the differences between the programs at the schools that cause such different enrollment numbers?
Also, the passing rate varies wildly between the schools, just look at AHS vs BAHS for environmental science:
AHS : BAHS:
Enrolled: 69 : 69
Tested: 70 : 23
Passed: 65 : 12
% Passed: 92.9% : 52.5%
What is going wrong at BAHS that half the class feels it is better to not take the test, are they worried about failing? And of those that take the test, why are half failing it, when AHS has every student in the class (plus I’d assume one independent study or a repeat) taking the test and only five failed. Have the teachers from the two schools shared their curriculum, lesson plans, assignments, etc? AHS and BAHS have similar passing rates for other tests, so it isn’t all about the quality of the students.
It is too unbalanced to compare BAHS with AHS. AHS (and Havre de Grace HS) had the NMSI program last year for all science, math and English courses. Between January and May there are study sessions every Saturday from 8:30-2:30-that were basically mandatory to attend, along with after-school sessions. Every student who gets a ‘3’ or better gets paid, as do the teachers. Lots of incentive to teach to the test, and to take it and study and do well.